Усереднити, щоб зміряти...
 | Продовжуючи розмову про елементи фінансового аналізу, зупинимося на понятті ануїтету, методах його оцінки, їх реалізації в Excel. Можливо, деякі моменти вам видадуться незвичними. Проте не поспішайте ставити їх під сумнів, а краще випробуйте на практиці. Оцінка майбутніх витрат за справжньою вартістю, перехід до середньоперіодичних значень дає набагато адекватнішу картину, ніж звичайне калькулювання абсолютних значень. Адже від точності ваших оцінок може залежати успішність роботи всього підприємства. Микола КАРПЕНКО, канд. техн. наук, доцент кафедри прикладної математики та інформаційних технологій Харківської національної академії міського господарства Юрій ЦИГАНОК, головний редактор, сертифікований бухгалтер-практик (CAP) |
Послідовність періодичних рівновеликих виплат (надходжень) називають ануїтетом. Приклади ануїтету на практиці зустрічаються часто: перерахування процентів від депозиту на спеціальний рахунок, погашення кредиту рівними частинами, накопичувальні внески тощо. Нас, як завжди, цікавитиме оцінка поточної (реальної, дисконтованої) та майбутньої вартості ануїтету, її розрахунок у програмі Excel. Така оцінка цікава не тільки сама по собі. У фінансовому аналізі її часто розглядають як СЕРЕДНЬОПЕРІОДИЧНУ вартість операції. Ми застосуємо таку оцінку для визначення реальної вартості витрат на експлуатацію та капітальне відновлення основних засобів. Але спочатку потрібно розібратися з теорією питання.
Дисконтована вартість ануїтету
Отже, ануїтет — це послідовність однакових платежів Pi, які надходять через рівні проміжки часу (періоди чи інтервали). Кількість інтервалів дорівнює n, а норма дисконтування — r. Припустимо, що платежі розташовані в кінці інтервалів. Це означає, що для визначення поточної вартості слід продисконтувати ВСІ значення потоку платежів. Запишемо це у вигляді формули. Якщо P1 — значення суми в 1-му інтервалі, то її поточна вартість дорівнює: PV(P1) = P1(1 + r)-1. Реальна вартість суми Pn в інтервалі n складе: PV(Pn) = P1(1 + r)-n. Щоб визначити реальну вартість усього потоку платежів, потрібно продисконтувати кожне його значення і підсумувати результат, тобто:
(1)
![]()
В ануїтеті всі платежі рівні (P1 = P2 = ... = Pi = Р). Тому формулу (1) можна записати без операції підсумовування:
(2)
![]()
Важливо!
ВеличинуНагадаємо, що у формулі (2) виконується дисконтування ВСІХ сум, які створюють потік платежів. Однак бувають ситуації, коли дисконтування першого елемента робити не потрібно. Прикладом може бути передоплата — вона здійснюється в початковий момент часу, її вартість є «поточною» за визначенням. У такому разі формула для поточної вартості потоку платежів дещо зміниться і виглядатиме так:
(3)
![]()
Мабуть, на цьому короткий екскурс у теоретичні нетрі можна завершити. Час «спуститися на землю» і подивитися, як можна застосувати все це на практиці. І заразом переконатися, що для роботи двоповерхові формули пам’ятати зовсім не обов’язково. Достатньо зрозуміти механізм їх дії, сферу застосування та своєчасно звернутися до вбудованої функції Excel. Це ми і зробимо на таких прикладах.
Ануїтетні платежі та довгострокові кредити
Роботу з ануїтетом найнаочніше можна показати на прикладі платежів за кредит.
Важливо!
Зараз ми говоримо не про якісь конкретні умови видачі кредиту. Нас цікавить схема нарахування складних процентів як така. Зокрема, механізм визначення величини виплат та реальної вартості всього потоку платежів.Отже, надаючи кредит, банк розраховує на отримання компенсації, пов’язаної з ризиком його непогашення і знеціненням майбутніх доходів (у вигляді платежів за кредит). Розмір цієї компенсації визначається процентною ставкою r. З точки зору кредитора
реальна вартість майбутніх виплат за кредитом, дисконтована під процентну ставку r, повинна бути не менше суми виданого кредиту. Інакше кредитор зазнає збитків.Припустимо, що кредит, виданий під r процентів на n періодів за умови одноразового погашення наприкінці строку. Відомо, що розмір виплати складе F. Тоді гранична сума кредиту, що видається, є не що інше, як реальна вартість майбутньої виплати, тобто: PV = F (1 + r)-n. Тепер перейдемо до ситуації, коли кредит видано під складний процент за умови рівномірного погашення рівними сумами протягом усього періоду. У цьому випадку платежі за кредитом є ануїтетом. Реальна вартість ануїтету визначається за формулою (1). Дотримуючись тієї ж логіки, що й при одноразовому погашенні, цю формулу можна використовувати для визначення граничної суми кредиту, яку можна взяти під r процентів на n періодів, якщо відомий розмір періодичних виплат. Усе викладене краще показати на конкретному прикладі.
Приклад
. Ми маємо намір узяти кредит на півроку і щомісячно погашати його сумами в розмірі 500 грн. Якою може бути сума кредиту, якщо процентна ставка становить 0,5 % на місяць?Результат розрахунків наведено на рис. 1. У перших трьох рядках таблиці розміщено вихідні дані: ставка, кількість періодів та розмір періодичної виплати, що передбачається.
У комірці «
B4» записана формула для визначення реальної вартості ануїтету із шести виплат по 500 грн. Текст формули зазначено в комірці «C4». У комірці «С5» можна побачити другий варіант розрахунку реальної вартості з використанням вбудованої функції «ПС()». У цієї функції п’ять параметрів: «ПС(r;n;P;Fv;Тип)», а саме:— «
r», процентна ставка за період;— «
n», кількість періодів;— «
P», розмір періодичної виплати, який залишається незмінним протягом усього періоду погашення;— «
Fv», майбутня вартість ануїтету після погашення, у нашому випадку «Fv» є залишком заборгованості після погашення, за умовчанням «Fv=0»;— «
Тип», зазначає, коли проводяться виплати, «Тип=0» — виплати знаходяться в кінці інтервалів, «Тип=1» — виплати розташовані на початку інтервалів.Із цих параметрів обов’язковими є перші три. Повернемося, наприклад, на рис. 1. Формула «
=-ПС(B1;B2;B3)» повертає значення «2948,19». Знак «-» у формулі поставлено не випадково. За логікою розробників Excel функція «ПС()» повертає поточну вартість ІНВЕСТИЦІЇ, тобто загальну суму, вартість якої на цей момент рівноцінна послідовності майбутніх ВИПЛАТ. Тому функція повертає від’ємне значення. У блоці таблиці «A7:E12» розгорнено показано механізм погашення кредиту за обраних умов. Первісна сума (за нашими розрахунками) склала 2948,19 грн. Це значення записано в комірці «B8». У колонці «Долг на конец периода» видно значення поточної заборгованості, розрахункова формула для першого періоду: «=B8*(1+$B$1)». Із цієї суми віднімаємо розмір періодичного платежу, він дорівнює 500 грн. Результат видно в колонці «Остаток». Наприклад, для першого періоду він дорівнює 2962,93 - 500 = 2462,93, а формула в «Е8» виглядає так: «=ОКРУГЛ(C8-D8;2)». Значення з «Е8» переходять до комірки «B9», у ній знаходиться формула «=E8». І далі розрахунок повторюється шість разів. Як ми і припускали, після останньої виплати заборгованість дорівнюватиме «0» (комірка «E13»). 
Змінимо вміст у «
B4», записавши туди формулу для майбутньої вартості ануїтету: «=-ПС(B1;B2;B3;100)». Результат роботи формули — «3045,24». Підставляємо це значення як первісну суму до комірки «B8». У «E13» бачимо залишок заборгованості в розмірі 100 грн.Важливо!
Формула реальної вартості ануїтету (2) дозволяє дізнатися, на яку суму можна взяти кредит, якщо відомі умови кредитування та розмір періодичних платежів.Для роботи з ануїтетом в Excel є й інші функції. Наприклад, нас може зацікавити таке запитання. Відома процентна ставка, розмір періодичного платежу, сума кредиту. За який період можливе погашення заборгованості за цих умов? У термінах формули (2) нам відомі «
PV», «Р», «r», а потрібно знайти «n». Для такого випадку в Excel передбачено функцію «КПЕР()». Наприклад, формула «=КПЕР(B1;-500,28;B8)» поверне значення «6». Тобто кредит у розмірі 2948,19 грн. можна погасити платежами по 500 грн. за шість місяців (процентна ставка 0,005 за період).Повернемося до таблиці на рис. 1. Робимо активною комірку «
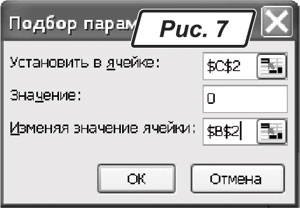
E11». Викликаємо «Сервис → Подбор параметра». Заповнюємо форму діалогу, як показано на рис. 2. Наша мета — знайти розмір платежу, який забезпечить погашення кредиту за заданих умов за 4 місяці. Вирішивши рівняння, Excel покаже значення: 746,28 грн. Цей же результат можна отримати функцією «=ПЛТ(B1;4;B8)». 
Важливо!
Зверніть увагу на знак «-» перед значенням періодичного платежу.Логічно припустити, що в Excel є і функція для визначення процентної ставки ануїтету, якщо відома сума, платіж та кількість періодів. Ця функція називається «Ставка()». Так, формула «=СТАВКА(B2;B3;-B8)» (рис. 1) поверне значення 0,005 (0,5 % за період).
З реальною вартістю ануїтету зрозуміло. Тепер подивимося на зворотну залежність, її прийнято позначати РА (Р, r, n):
(3)
![]()
Ця формула дозволяє дізнатися про РОЗМІР ПЛАТЕЖУ за відомих умов кредитування. В Excel їй відповідає функція «ПЛТ()». Наприклад, щоб визначити розмір платежу за даними таблиці на рис. 1, можна скористатися формулою: «=ПЛТ(B1;B2;B8)». Результат її роботи — «-500».
Оцінка експлуатаційних витрат
Експлуатаційні витрати (ЕВ) зазвичай виникають періодично (планово-запобіжні ремонти тощо) і розподілені на значний проміжок часу. До моменту використання кошти для покриття ЕВ можуть знаходитися в обороті, забезпечуючи дохід у вигляді процента на вкладений капітал. Тому реальна величина експлуатаційних витрат менше свого абсолютного значення на величину цього потенційного прибутку.
Важливо!
Оцінку реальної вартості експлуатаційних витрат, які рівномірно розподілені протягом деякого періоду, можна здійснити за формулою (2). В Excel для цього використовують функцію «ПС()».Цей факт можна прокоментувати і таким чином. Ми знаємо, що строк експлуатації устаткування становить n періодів, середньоперіодичні витрати на експлуатацію дорівнюють P, а норма дисконтування r. Логічно запитати: скільки коштів потрібно покласти на депозит під r процентів, щоб протягом n періодів знімати суму P і направляти її на погашення експлуатаційних витрат? Величина цього внеску і буде реальною оцінкою вартості експлуатації. А визначити її можна за формулою (2).
Приклад
. На лудіння устаткування витрачається 25000 грн. щоквартально. Яка реальна величина експлуатаційних витрат в перерахунку на 1 рік при нормі дисконтування 10 % за період? Результати розрахунку наведено на рис. 3. Для визначення реальної вартості використано формулу «=-ПС(C3;C2;C1)». Абсолютна величина експлуатаційних витрат становить 25000 х 4 = 100000 грн., тоді як їх реальна вартість на 20753,36 грн. менше. Докладно принцип визначення реальної вартості розписано у блоці «A7:E10»: нам СЬОГОДНІ потрібно мати 79246,64 грн. з тим, щоб внести їх під 10 % і протягом чотирьох періодів погашати витрати в розмірі 25000 грн. 
Оцінка витрат на капітальне відновлення
Особливістю витрат на капітальне відновлення (КВ) є те, що вони розраховані на тривалу перспективу, але здійснюються сьогодні. Отже, при інвестуванні в капітальне відновлення втрачається процент з обороту від загальної суми витрат. Тому реальна вартість капітального відновлення збільшується на величину цих витрат.
На практиці зазвичай є різні способи виконання робіт з капітального відновлення. Кожний із них характеризується певною сумою, забезпечує різний ступінь якості. Наприклад, відремонтувати будівлю можна дешевше, але ремонт буде недовговічним. Збільшивши витрати на відновлення, можна підвищити якість і відремонтувати будівлю надовго. Як у такому разі порівнювати величину капітальних витрат? Відповідь проста: визначити середньоперіодичну вартість капітального відновлення. Зробити це можна за формулою (3).
Виникає запитання: чому для оцінки вартості КВ використовується формула розрахунку періодичних платежів за кредит? У цьому немає нічого дивного. Уявимо, що на фінансування капітального відновлення спрямовано кредит, узятий під r процентів на n періодів. Тоді фактична вартість капітального відновлення повинна враховувати не тільки суму кредиту, а й проценти, що виплачено за нього. А розмір платежу за кредит можна розглядати як середньоперіодичну вартість капітального відновлення: адже сума платежу включає покриття і самого тіла кредиту, і нарахованих процентів.
Тепер абстрагуємося від кредиту. Припустимо, підприємство веде будівництво, вкладаючи в нього певну суму. Оскільки цю суму вилучають з обороту, підприємство втрачає можливість отримати прибуток від її використання. Якщо за один період рентабельність оборотних коштів становить r процентів, їх і буде втрачено. Отже, фактична величина витрат на будівництво повинна включати власне суму та втрачені проценти. При цьому немає жодної різниці, як саме ці проценти втрачаються: переходять вони кредитору чи потрапляють до розряду втрат унаслідок «омертвіння» капіталу. Тому для розрахунків і було використано формулу (3). А тепер невеликий приклад.
Приклад
. Є два варіанти капітального будівництва. Вартість першого варіанта (А) 1800 тис. грн. Він забезпечує строк служби споруди 30 років і вимагає щорічних витрат на утримання в розмірі 20 тис. грн. Другий варіант (В) коштує 450 тис. грн., витрати на експлуатацію складуть 80 тис. грн. на рік. Норма дисконтування дорівнює 7 % на рік. Визначити, який із запропонованих варіантів прийнятніший.Дані за варіантами наведено в таблиці на рис. 4. Щоб відповісти на поставлене запитання, потрібно обчислити середньоперіодичну величину витрат на капітальне відновлення в кожному з варіантів. Такий розрахунок зроблено в рядку номер п’ять. Так, для першого варіанта формула в комірці «
B5» виглядає так: «=-ПЛТ(0,07;B2;B3)». А загальна вартість варіанта — це сума середньоперіодичних витрат на КВ та витрат на експлуатацію, тобто «=B5+B4» (комірка «B6»). За даними нашого прикладу в першому варіанті витрати склали 165,06 грн. за період, а в другому — 144,07 грн. Кращим є варіант В. 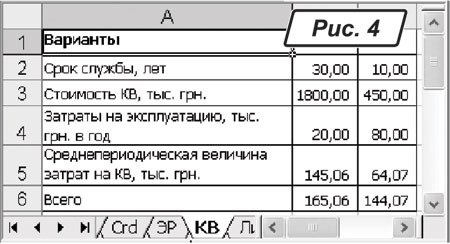
Порада
Щоб співставити варіанти капітального відновлення з різними строками експлуатації, порівняйте середньоперіодичну величину витрат за кожним із них та виберіть оптимальне рішення.
Загальні суми при рівномірних депозитах
Досі ми розглядали потоки платежів без «накопичувального ефекту». У практиці фінансового аналізу часто доводиться працювати з потоками платежів, які в кожному періоді збільшуються на постійну величину «
A». Для майбутньої вартості такого потоку платежів можна використовувати таку формулу:(4)
![]()
Її прийнято позначати FA (А, r, n). За цією формулою можна визначити, наприклад, сумарну заборгованість, якщо ми n разів позичали суму А під процент r. За цією формулою також можна знайти загальну суму, яка утворюється внаслідок періодичного поповнення депозиту внесками А протягом n періодів. Пояснимо механізм формування потоку платежів з рівномірними депозитами докладніше.
Приклад
. Визначити, якою буде загальна сума на рахунку через п’ять років, якщо він щорічно поповнюється на 10000 грн., а процентна ставка дорівнює 13 %?У таблиці на рис. 5 наведено схему нарахувань (рух коштів на рахунку) для цього потоку платежів. Для цього до комірки «
B2» записана початкова сума. У «C2» до цієї суми додано 13 %, тобто формула в «C2» така: «=B2*(1,13)». У кінці періоду ця сума збільшується на 10000 грн. (величину приросту записано в «D2»). Отриманий результат переходить на наступний період, тобто в «С3» зазначено формулу «=C2+D2». Процес повторюється до п’ятого періоду. Отже, за п’ять років буде накопичено суму 64802,71 грн. (комірка «B6»). 
Однак нас цікавить не гіпотетичний приклад з накопичувальним рахунком. Нам потрібна функція Excel для визначення загальної суми за зазначеним принципом нарахування. Ця функція називається «
БС()». Її синтаксис такий: «БС(r;n;А;Pv;Тип)». У цій функції «r» — процентна ставка за період, «n» — кількість періодів, «А» — періодичний платіж, «Pv» — поточна вартість деяких майбутніх виплат, «Тип» — ознака, указує, коли проводяться виплати. Якщо «Тип=0», виплати віднесено на кінець інтервалу, якщо «Тип=1», виплати розташовані на початку інтервалу. Скористаємося функцією, щоб визначити майбутню вартість потоку платежів з нашого прикладу. До комірки «B8» пишемо формулу «=-БС(0,13;5;10000)», результат її дорівнює 64802,71 грн.Зворотна залежність AF (F, r, n) дозволяє оцінити середньоперіодичну (!) вартість потоку платежів з рівномірними депозитами, майбутня вартість якого дорівнює F. Відповідна формула виглядає так:
(5)
![]()
Формула (5) дозволяє, наприклад, визначити розмір періодичної позики, якщо сумарна заборгованість через n періодів не повинна перевищити величину F. За цією формулою можна знайти, на скільки потрібно періодично поповнювати рахунок, щоб через n періодів на ньому накопичилася сума F.
Незважаючи на «грізний» вигляд, боятися формули не варто. Для визначення середньоперіодичної вартості потоку платежів при рівномірних депозитах в Excel є функція «
ПЛТ()». Скористаємося нею для нашого прикладу. Ми хочемо дізнатися, скільки потрібно перераховувати на депозит щорічно протягом 5 років під 13 % річних, щоб у результаті накопичити 64802,71 грн.? До комірки «B9» пишемо формулу «=-ПЛТ(0,13;5;0;64802,71)». Результат її роботи дорівнює 10000 грн.З механізмом нарахувань та функціями ми розібралися. Залишається показати, як це можна використовувати в реальній роботі.
Приклад
. Є два варіанти забезпечити підприємство транспортом. Перший — орендувати автомобіль із розрахунку 3,0 грн. за кілометр. Другий варіант — придбати його за 32500 грн. Передбачається, що машина працюватиме 5 років, після чого її буде продано за 16000 грн. На бензин та мастильні матеріали витрачається по 0,8 грн. на кілометр. Інші витрати становитимуть 1500 грн. на рік. Необхідно з’ясувати, при якому пробігу варіанти рівноцінні, якщо ставка дисконтування 10 %?Спочатку алгоритм розрахунку. Позначимо Х довжину пробігу в кілометрах. Тоді вартість першого варіанта (вона пропорційна пробігу) можна записати як «
3Х». Вартість другого варіанта визначимо так: «0,8Х+1500+AP (32500; 0,1; 5)-AF(16000; 0,1; 5)». Вона складається зі змінних витрат, вони залежать від тривалості пробігу («0,8Х»). До цих витрат ми додали інші витрати (1500 грн. на рік), середньоперіодичну вартість придбання автомобіля. Суму, що вийшла, зменшили на середньоперіодичне значення доходу від майбутньої реалізації автомобіля. Залишається об’єднати обидва вирази в одне рівняння і знайти Х. Усе, як у школі… У нашому випадку Х = 3387,57. Тобто при пробігу менше 3387,57 кілометрів кращим є перший варіант. При більшому пробігу перевагу має другий варіант.Тепер подивимося, як це виглядає в Excel. Заповнюємо таблицю, як на рис. 6. До «
B2» ставимо значення пробігу, спочатку воно може бути довільним. Формула для розрахунку вартості в першому варіанті («=B2*B3») знаходиться в комірці «B4». Другий варіант дещо складніше. Вартість ПММ, що залежить від пробігу, обчислена в комірці «B9», формула розрахунку — «=B8*B7». Оцінка витрат на придбання транспортного засобу знаходиться в «B14», формула для розрахунку — «=-ПЛТ(B11;B12;B13)». Оцінка доходу від реалізації автомобіля після п’ятирічного періоду експлуатації знаходиться в комірці «B16», її обчислено за формулою «=ПЛТ(B11;B12;0;B15)». Сумарна вартість другого варіанта складає «=B16+B14+B10+B9» (комірка «B17»). Залишається знайти граничну величину пробігу. Зробимо це інструментом «Подбор параметра». У комірці «С2» зазначаємо формулу «=B17-B4». Викликаємо меню «Сервис → Подбор параметра…». У вікні, що з’явилося, заповнюємо параметри, як показано на рис. 7. Натискуємо «ОК», у комірці «С2» з’явиться рішення: 3387,57 км. Графічну ілюстрацію цих розрахунків наведено на рис. 8. 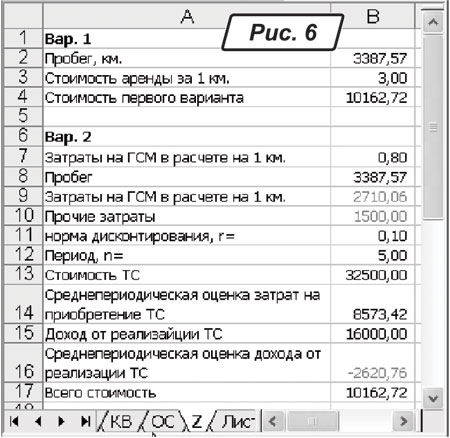

На цьому завершимо перше знайомство з елементами фінансового аналізу на ПК. У наступних статтях на цю тему розглянемо врахування факторів ризику та розрахунок строків окупності.
А поки що бажаємо успішно застосувати отримані навички на практиці. Чекаємо на ваші запитання, листи, пропозиції та зауваження на bk@id.factor.ua, nictomkar@rambler.ru або на форумі редакції
www.bk.factor.ua/forum .Успішної роботи!







